SciPy Spatial Data
Working with Spatial Data
Spatial data refers to data that is represented in a geometric space.
E.g. points on a coordinate system.
We deal with spatial data problems on many tasks.
E.g. finding if a point is inside a boundary or not.
SciPy provides us with the module scipy.spatial, which has
functions for working with
spatial data.
Triangulation
A Triangulation of a polygon is to divide the polygon into multiple triangles with which we can compute an area of the polygon.
A Triangulation with points means creating surface composed triangles in which all of the given points are on at least one vertex of any triangle in the surface.
One method to generate these triangulations through points is the Delaunay() Triangulation.
Example
Create a triangulation from following points:
import numpy as np
from scipy.spatial import Delaunay
import matplotlib.pyplot as plt
points = np.array([
[2, 4],
[3, 4],
[3, 0],
[2, 2],
[4, 1]
])
simplices = Delaunay(points).simplices
plt.triplot(points[:, 0], points[:, 1], simplices)
plt.scatter(points[:, 0], points[:, 1], color='r')
plt.show()
Result:
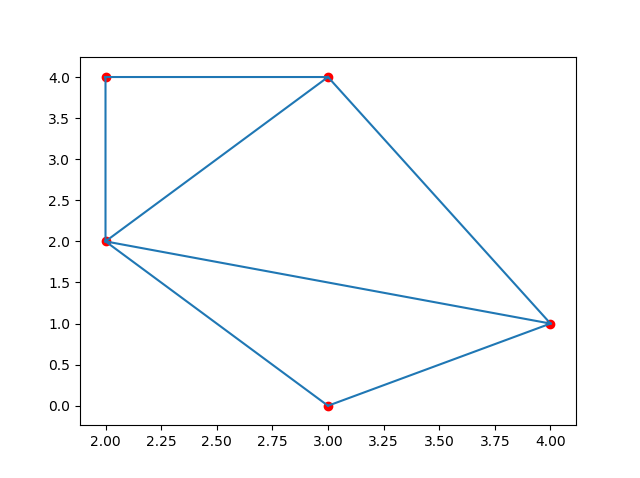
Note: The simplices property creates a generalization of the triangle notation.
Convex Hull
A convex hull is the smallest polygon that covers all of the given points.
Use the ConvexHull() method to create a Convex Hull.
Example
Create a convex hull for following points:
import numpy as np
from scipy.spatial import ConvexHull
import matplotlib.pyplot as plt
points = np.array([
[2, 4],
[3, 4],
[3, 0],
[2, 2],
[4, 1],
[1, 2],
[5, 0],
[3, 1],
[1, 2],
[0, 2]
])
hull = ConvexHull(points)
hull_points = hull.simplices
plt.scatter(points[:,0], points[:,1])
for simplex in hull_points:
plt.plot(points[simplex,0], points[simplex,1], 'k-')
plt.show()
Result:
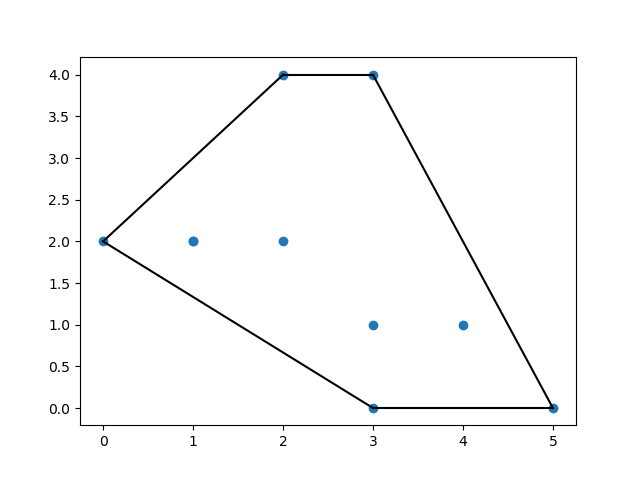
KDTrees
KDTrees are a datastructure optimized for nearest neighbor queries.
E.g. in a set of points using KDTrees we can efficiently ask which points are nearest to a certain given point.
The KDTree() method returns a KDTree object.
The query() method returns the distance to the nearest neighbor and
the location of the neighbors.
Example
Find the nearest neighbor to point (1,1):
from scipy.spatial import KDTree
points = [(1, -1), (2, 3), (-2, 3), (2, -3)]
kdtree = KDTree(points)
res = kdtree.query((1, 1))
print(res)
Result:
(2.0, 0)Try it Yourself »
Distance Matrix
There are many Distance Metrics used to find various types of distances between two points in data science, Euclidean distsance, cosine distsance etc.
The distance between two vectors may not only be the length of straight line between them, it can also be the angle between them from origin, or number of unit steps required etc.
Many of the Machine Learning algorithm's performance depends greatly on distance metrices. E.g. "K Nearest Neighbors", or "K Means" etc.
Let us look at some of the Distance Metrices:
Euclidean Distance
Find the euclidean distance between given points.
Example
from scipy.spatial.distance import euclidean
p1 = (1, 0)
p2 = (10, 2)
res = euclidean(p1, p2)
print(res)
Result:
9.21954445729Try it Yourself »
Cityblock Distance (Manhattan Distance)
Is the distance computed using 4 degrees of movement.
E.g. we can only move: up, down, right, or left, not diagonally.
Example
Find the cityblock distance between given points:
from scipy.spatial.distance import cityblock
p1 = (1, 0)
p2 = (10, 2)
res = cityblock(p1, p2)
print(res)
Result:
11Try it Yourself »
Cosine Distance
Is the value of cosine angle between the two points A and B.
Example
Find the cosine distsance between given points:
from scipy.spatial.distance import cosine
p1 = (1, 0)
p2 = (10, 2)
res = cosine(p1, p2)
print(res)
Result:
0.019419324309079777Try it Yourself »
Hamming Distance
Is the proportion of bits where two bits are different.
It's a way to measure distance for binary sequences.
Example
Find the hamming distance between given points:
from scipy.spatial.distance import hamming
p1 = (True, False, True)
p2 = (False, True, True)
res = hamming(p1, p2)
print(res)
Result:
0.666666666667Try it Yourself »

