DSA Counting Sort with Python
Counting Sort
The Counting Sort algorithm sorts an array by counting the number of times each value occurs.
{{ msgDone }}
Run the simulation to see how 17 integer values from 1 till 5 are sorted using Counting Sort.
Counting Sort does not compare values like the previous sorting algorithms we have looked at, and only works on non negative integers.
Furthermore, Counting Sort is fast when the range of possible values \(k\) is smaller than the number of values \(n\).
How it works:
- Create a new array for counting how many there are of the different values.
- Go through the array that needs to be sorted.
- For each value, count it by increasing the counting array at the corresponding index.
- After counting the values, go through the counting array to create the sorted array.
- For each count in the counting array, create the correct number of elements, with values that correspond to the counting array index.
Conditions for Counting Sort
These are the reasons why Counting Sort is said to only work for a limited range of non-negative integer values:
- Integer values: Counting Sort relies on counting occurrences of distinct values, so they must be integers. With integers, each value fits with an index (for non negative values), and there is a limited number of different values, so that the number of possible different values \(k\) is not too big compared to the number of values \(n\).
- Non negative values: Counting Sort is usually implemented by creating an array for counting. When the algorithm goes through the values to be sorted, value x is counted by increasing the counting array value at index x. If we tried sorting negative values, we would get in trouble with sorting value -3, because index -3 would be outside the counting array.
- Limited range of values: If the number of possible different values to be sorted \(k\) is larger than the number of values to be sorted \(n\), the counting array we need for sorting will be larger than the original array we have that needs sorting, and the algorithm becomes ineffective.
Manual Run Through
Before we implement the Counting Sort algorithm in a programming language, let's manually run through a short array, just to get the idea.
Step 1: We start with an unsorted array.
myArray = [ 2, 3, 0, 2, 3, 2]
Step 2: We create another array for counting how many there are of each value. The array has 4 elements, to hold values 0 through 3.
myArray = [ 2, 3, 0, 2, 3, 2]
countArray = [ 0, 0, 0, 0]
Step 3: Now let's start counting. The first element is 2, so we must increment the counting array element at index 2.
myArray = [ 2, 3, 0, 2, 3, 2]
countArray = [ 0, 0, 1, 0]
Step 4: After counting a value, we can remove it, and count the next value, which is 3.
myArray = [ 3, 0, 2, 3, 2]
countArray = [ 0, 0, 1, 1]
Step 5: The next value we count is 0, so we increment index 0 in the counting array.
myArray = [ 0, 2, 3, 2]
countArray = [ 1, 0, 1, 1]
Step 6: We continue like this until all values are counted.
myArray = [ ]
countArray = [ 1, 0, 3, 2]
Step 7: Now we will recreate the elements from the initial array, and we will do it so that the elements are ordered lowest to highest.
The first element in the counting array tells us that we have 1 element with value 0. So we push 1 element with value 0 into the array, and we decrease the element at index 0 in the counting array with 1.
myArray = [ 0]
countArray = [ 0, 0, 3, 2]
Step 8: From the counting array we see that we do not need to create any elements with value 1.
myArray = [ 0]
countArray = [ 0, 0, 3, 2]
Step 9: We push 3 elements with value 2 into the end of the array. And as we create these elements we also decrease the counting array at index 2.
myArray = [ 0, 2, 2, 2]
countArray = [ 0, 0, 0, 2]
Step 10: At last we must add 2 elements with value 3 at the end of the array.
myArray = [0, 2, 2, 2, 3, 3]
countArray = [ 0, 0, 0, 0]
Finally! The array is sorted.
Run the simulation below to see the steps above animated:
countArray = [
Implement Counting Sort in Python
To implement the Counting Sort algorithm in a Python program, we need:
- An array with values to sort.
- A 'countingSort' method that receives an array of integers.
- An array inside the method to keep count of the values.
- A loop inside the method that counts and removes values, by incrementing elements in the counting array.
- A loop inside the method that recreates the array by using the counting array, so that the elements appear in the right order.
One more thing: We need to find out what the highest value in the array is, so that the counting array can be created with the correct size. For example, if the highest value is 5, the counting array must be 6 elements in total, to be able count all possible non negative integers 0, 1, 2, 3, 4 and 5.
The resulting code looks like this:
Example
Using the Counting Sort algorithm in a Python program:
def countingSort(arr):
max_val = max(arr)
count = [0] * (max_val + 1)
while len(arr) > 0:
num = arr.pop(0)
count[num] += 1
for i in range(len(count)):
while count[i] > 0:
arr.append(i)
count[i] -= 1
return arr
mylist = [4, 2, 2, 6, 3, 3, 1, 6, 5, 2, 3]
mysortedlist = countingSort(mylist)
print(mysortedlist)
Run Example »
Counting Sort Time Complexity
How fast the Counting Sort algorithm runs depends on both the range of possible values \(k\) and the number of values \(n\).
In general, time complexity for Counting Sort is \(O(n+k)\).
In a best case scenario, the range of possible different values \(k\) is very small compared to the number of values \(n\) and Counting Sort has time complexity \(O(n)\).
But in a worst case scenario, the range of possible different values \(k\) is very big compared to the number of values \(n\) and Counting Sort can have time complexity \(O(n^2)\) or even worse.
The plot below shows how much the time complexity for Counting Sort can vary.
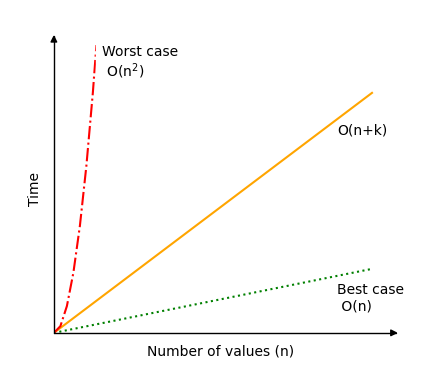
As you can see, it is important to consider the range of values compared to the number of values to be sorted before choosing Counting Sort as your algorithm. Also, as mentioned at the top of the page, keep in mind that Counting Sort only works for non negative integer values.
As mentioned previously: if the numbers to be sorted varies a lot in value (large \(k\)), and there are few numbers to sort (small \(n\)), the Counting Sort algorithm is not effective.
If we hold \(n\) and \(k\) fixed, the "Random", "Descending" and "Ascending" alternatives in the simulation above results in the same number of operations. This is because the same thing happens in all three cases: A counting array is set up, the numbers are counted, and the new sorted array is created.

