Data Science - Statistics Standard Deviation
Standard Deviation
Standard deviation is a number that describes how spread out the observations are.

A mathematical function will have difficulties in predicting precise values, if the observations are "spread". Standard deviation is a measure of uncertainty.
A low standard deviation means that most of the numbers are close to the mean (average) value.
A high standard deviation means that the values are spread out over a wider range.
Tip: Standard Deviation is often represented by the symbol Sigma: σ
We can use the std() function from Numpy to find the standard deviation of a variable:
The output:
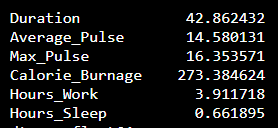
What does these numbers mean?
Coefficient of Variation
The coefficient of variation is used to get an idea of how large the standard deviation is.
Mathematically, the coefficient of variation is defined as:
Coefficient of Variation = Standard Deviation / Mean
We can do this in Python if we proceed with the following code:
Example
import numpy as np
cv = np.std(full_health_data) / np.mean(full_health_data)
print(cv)
Try it Yourself »
The output:
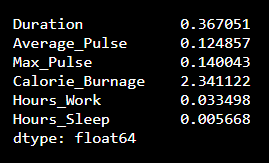
We see that the variables Duration, Calorie_Burnage and Hours_Work has a high Standard Deviation compared to Max_Pulse, Average_Pulse and Hours_Sleep.

