Perceptrons
A Perceptron is an Artificial Neuron
It is the simplest possible Neural Network
Neural Networks are the building blocks of Machine Learning.
Frank Rosenblatt
Frank Rosenblatt (1928 – 1971) was an American psychologist notable in the field of Artificial Intelligence.
In 1957 he started something really big. He "invented" a Perceptron program, on an IBM 704 computer at Cornell Aeronautical Laboratory.
Scientists had discovered that brain cells (Neurons) receive input from our senses by electrical signals.
The Neurons, then again, use electrical signals to store information, and to make decisions based on previous input.
Frank had the idea that Perceptrons could simulate brain principles, with the ability to learn and make decisions.
The Perceptron
The original Perceptron was designed to take a number of binary inputs, and produce one binary output (0 or 1).
The idea was to use different weights to represent the importance of each input, and that the sum of the values should be greater than a threshold value before making a decision like yes or no (true or false) (0 or 1).
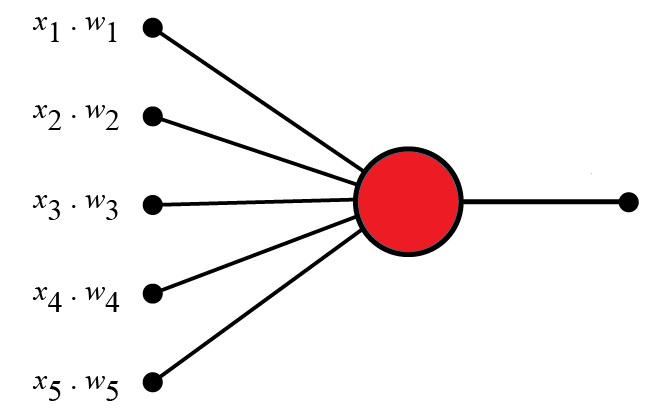
Perceptron Example
Imagine a perceptron (in your brain).
The perceptron tries to decide if you should go to a concert.
Is the artist good? Is the weather good?
What weights should these facts have?
| Criteria | Input | Weight |
|---|---|---|
| Artists is Good | x1 = 0 or 1 | w1 = 0.7 |
| Weather is Good | x2 = 0 or 1 | w2 = 0.6 |
| Friend will Come | x3 = 0 or 1 | w3 = 0.5 |
| Food is Served | x4 = 0 or 1 | w4 = 0.3 |
| Alcohol is Served | x5 = 0 or 1 | w5 = 0.4 |
The Perceptron Algorithm
Frank Rosenblatt suggested this algorithm:
- Set a threshold value
- Multiply all inputs with its weights
- Sum all the results
- Activate the output
1. Set a threshold value:
- Threshold = 1.5
2. Multiply all inputs with its weights:
- x1 * w1 = 1 * 0.7 = 0.7
- x2 * w2 = 0 * 0.6 = 0
- x3 * w3 = 1 * 0.5 = 0.5
- x4 * w4 = 0 * 0.3 = 0
- x5 * w5 = 1 * 0.4 = 0.4
3. Sum all the results:
- 0.7 + 0 + 0.5 + 0 + 0.4 = 1.6 (The Weighted Sum)
4. Activate the Output:
- Return true if the sum > 1.5 ("Yes I will go to the Concert")
Note
If the weather weight is 0.6 for you, it might be different for someone else. A higher weight means that the weather is more important to them.
If the threshold value is 1.5 for you, it might be different for someone else. A lower threshold means they are more wanting to go to any concert.
Example
const threshold = 1.5;
const inputs = [1, 0, 1, 0, 1];
const weights = [0.7, 0.6, 0.5, 0.3, 0.4];
let sum = 0;
for (let i = 0; i < inputs.length; i++) {
sum += inputs[i] * weights[i];
}
const activate = (sum > 1.5);
Perceptron in AI
A Perceptron is an Artificial Neuron.
It is inspired by the function of a Biological Neuron.
It plays a crucial role in Artificial Intelligence.
It is an important building block in Neural Networks.
To understand the theory behind it, we can break down its components:
- Perceptron Inputs (nodes)
- Node values (1, 0, 1, 0, 1)
- Node Weights (0.7, 0.6, 0.5, 0.3, 0.4)
- Activation Function
- Treshold Value
- Summation (sum > treshold)
Perceptron Inputs
A perceptron receives one or more input.
Perceptron inputs are called nodes.
The nodes have both a value and a weight.
Node Values (Input Values)
Input nodes have a binary value of 1 or 0.
This can be interpreted as true or false / yes or no.
In the example above, the node values are: 1, 0, 1, 0, 1
Node Weights
Weights are values assigned to each input.
Weights shows the strength of each node.
A higher value means that the input has a stronger influence on the output.
In the example above, the node weights are: 0.7, 0.6, 0.5, 0.3, 0.4
Summation
The perceptron calculates the weighted sum of its inputs.
It multiplies each input by its corresponding weight and sums up the results.
In the example above, the sum is: 0.7 + 0 + 0.5 + 0 + 0.4 = 1.6
The Activation Function
After the summation, the perceptron applies an activation function to the sum.
The purpose is to introduce non-linearity into the output. It determines whether the perceptron should fire or not based on the aggregated input.
In the example above, the activation function is simple: (sum > 1.5)
The Threshold
The activation function is typically accompanied by a Threshold Value.
If the result of the activation function exceeds the threshold, the perceptron fires (outputs 1), otherwise it remains inactive (outputs 0).
In the example above, the treshold value is: 1.5
The Output
The final output of the perceptron is the result of the activation function.
It represents the perceptron's decision or prediction based on the input and the weights.
The activation function maps the the weighted sum into a binary value.
The binary 1 or 0 can be interpreted as true or false / yes or no.
In the example above. the output is 1 because: (sum > 1.5) or (1.6 > 1.5).
Perceptron Learning
The perceptron can learn from examples through a process called training.
During training, the perceptron adjusts its weights based on observed errors. This is typically done using a learning algorithm such as the perceptron learning rule or a backpropagation algorithm.
The learning process presents the perceptron with labeled examples, where the desired output is known. The perceptron compares its output with the desired output and adjusts its weights accordingly, aiming to minimize the error between the predicted and desired outputs.
The learning process allows the perceptron to learn the weights that enable it to make accurate predictions for new, unknown inputs.
Note
It is obvious a decisions can NOT be made by One Neuron alone.
Other neurons must provide more input:
- Is the artist good
- Is the weather good
- ...
Multi-Layer Perceptrons can be used for more sophisticated decision making.
It's important to note that while perceptrons were influential in the development of artificial neural networks, they are limited to learning linearly separable patterns.
However, by stacking multiple perceptrons together in layers and incorporating non-linear activation functions, neural networks can overcome this limitation and learn more complex patterns.
Neural Networks
The Perceptron defines the first step into Neural Networks:
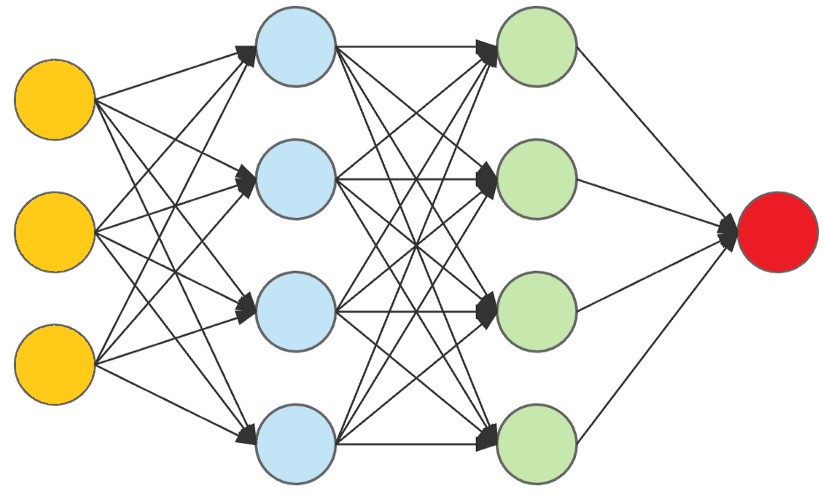
Perceptrons are often used as the building blocks for more complex neural networks, such as multi-layer perceptrons (MLPs) or deep neural networks (DNNs).
By combining multiple perceptrons in layers and connecting them in a network structure, these models can learn and represent complex patterns and relationships in data, enabling tasks such as image recognition, natural language processing, and decision making.
