DSA Binary Search
Binary Search
The Binary Search algorithm searches through an array and returns the index of the value it searches for.
Speed:
Current value: {{ currVal }}
{{ msgDone }}Run the simulation to see how the Binary Search algorithm works.
Too see what happens when a value is not found, try to find value 5.
Binary Search is much faster than Linear Search, but requires a sorted array to work.
The Binary Search algorithm works by checking the value in the center of the array. If the target value is lower, the next value to check is in the center of the left half of the array. This way of searching means that the search area is always half of the previous search area, and this is why the Binary Search algorithm is so fast.
This process of halving the search area happens until the target value is found, or until the search area of the array is empty.
How it works:
- Check the value in the center of the array.
- If the target value is lower, search the left half of the array. If the target value is higher, search the right half.
- Continue step 1 and 2 for the new reduced part of the array until the target value is found or until the search area is empty.
- If the value is found, return the target value index. If the target value is not found, return -1.
Manual Run Through
Let's try to do the searching manually, just to get an even better understanding of how Binary Search works before actually implementing it in a programming language. We will search for value 11.
Step 1: We start with an array.
[ 2, 3, 7, 7, 11, 15, 25]
Step 2: The value in the middle of the array at index 3, is it equal to 11?
[ 2, 3, 7, 7, 11, 15, 25]
Step 3: 7 is less than 11, so we must search for 11 to the right of index 3. The values to the right of index 3 are [ 11, 15, 25]. The next value to check is the middle value 15, at index 5.
[ 2, 3, 7, 7, 11, 15, 25]
Step 4: 15 is higher than 11, so we must search to the left of index 5. We have already checked index 0-3, so index 4 is only value left to check.
[ 2, 3, 7, 7, 11, 15, 25]
We have found it!
Value 11 is found at index 4.
Returning index position 4.
Binary Search is finished.
Run the simulation below to see the steps above animated:
Manual Run Through: What Happened?
To start with, the algorithm has two variables "left" and "right".
"left" is 0 and represents the index of the first value in the array, and "right" is 6 and represents the index of the last value in the array.
\((left+right)/2=(0+6)/2=3\) is the first index used to check if the middle value (7) is equal to the target value (11).
7 is lower than the target value 11, so in the next loop the search area must be limited to the right side of the middle value: [ 11, 15, 25], on index 4-6.
To limit the search area and find a new middle value, "left" is updated to index 4, "right" is still 6. 4 and 6 are the indexes for the first and last values in the new search area, the right side of the previous middle value. The new middle value index is \((left+right)/2=(4+6)/2=10/2=5\).
The new middle value on index 5 is checked: 15 is higher than 11, so if the target value 11 exists in the array it must be on the left side of index 5. The new search area is created by updating "right" from 6 to 4. Now both "left" and "right" is 4, \((left+right)/2=(4+4)/2=4\), so there is only index 4 left to check. The target value 11 is found at index 4, so index 4 is returned.
In general, this is the way the Binary Search algorithm continues to halve the array search area until the target value is found.
When the target value is found, the index of the target value is returned. If the target value is not found, -1 is returned.
Binary Search Implementation
To implement the Binary Search algorithm we need:
- An array with values to search through.
- A target value to search for.
- A loop that runs as long as left index is less than, or equal to, the right index.
- An if-statement that compares the middle value with the target value, and returns the index if the target value is found.
- An if-statement that checks if the target value is less than, or larger than, the middle value, and updates the "left" or "right" variables to narrow down the search area.
- After the loop, return -1, because at this point we know the target value has not been found.
The resulting code for Binary Search looks like this:
Example
def binarySearch(arr, targetVal):
left = 0
right = len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == targetVal:
return mid
if arr[mid] < targetVal:
left = mid + 1
else:
right = mid - 1
return -1
myArray = [1, 3, 5, 7, 9, 11, 13, 15, 17, 19]
myTarget = 15
result = binarySearch(myArray, myTarget)
if result != -1:
print("Value",myTarget,"found at index", result)
else:
print("Target not found in array.")Binary Search Time Complexity
For a general explanation of what time complexity is, visit this page.
For a more thorough and detailed explanation of Insertion Sort time complexity, visit this page.
Each time Binary Search checks a new value to see if it is the target value, the search area is halved.
This means that even in the worst case scenario where Binary Search cannot find the target value, it still only needs \( \log_{2}n \) comparisons to look through a sorted array of \(n\) values.
Time complexity for Binary Search is
\[ O( \log_{2} n ) \]
Note: When writing time complexity using Big O notation we could also just have written \( O( \log n ) \), but \( O( \log_{2} n ) \) reminds us that the array search area is halved for every new comparison, which is the basic concept of Binary Search, so we will just keep the base 2 indication in this case.
If we draw how much time Binary Search needs to find a value in an array of \(n\) values, compared to Linear Search, we get this graph:
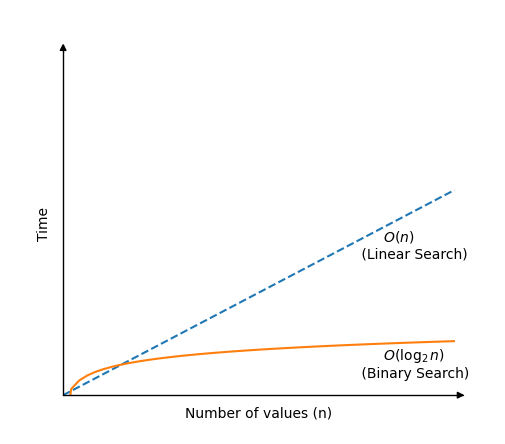
Run the Binary Search simulation below for different number of values \(n\) in an array, and see how many compares are needed for Binary Search to find the target value:
{{ this.userX }}
Operations: {{ operations }}
Not found!
As you can see when running simulations of Binary Search, the search requires very few compares, even if the the array is big and the value we are looking for is not found.

