DSA Merge Sort
Merge Sort
The Merge Sort algorithm is a divide-and-conquer algorithm that sorts an array by first breaking it down into smaller arrays, and then building the array back together the correct way so that it is sorted.
Speed:
{{ msgDone }}Divide: The algorithm starts with breaking up the array into smaller and smaller pieces until one such sub-array only consists of one element.
Conquer: The algorithm merges the small pieces of the array back together by putting the lowest values first, resulting in a sorted array.
The breaking down and building up of the array to sort the array is done recursively.
In the animation above, each time the bars are pushed down represents a recursive call, splitting the array into smaller pieces. When the bars are lifted up, it means that two sub-arrays have been merged together.
The Merge Sort algorithm can be described like this:
How it works:
- Divide the unsorted array into two sub-arrays, half the size of the original.
- Continue to divide the sub-arrays as long as the current piece of the array has more than one element.
- Merge two sub-arrays together by always putting the lowest value first.
- Keep merging until there are no sub-arrays left.
Take a look at the drawing below to see how Merge Sort works from a different perspective. As you can see, the array is split into smaller and smaller pieces until it is merged back together. And as the merging happens, values from each sub-array are compared so that the lowest value comes first.
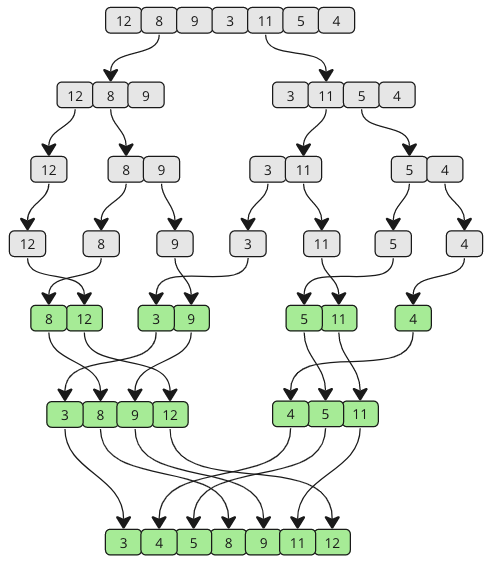
Manual Run Through
Let's try to do the sorting manually, just to get an even better understanding of how Merge Sort works before actually implementing it in a programming language.
Step 1: We start with an unsorted array, and we know that it splits in half until the sub-arrays only consist of one element. The Merge Sort function calls itself two times, once for each half of the array. That means that the first sub-array will split into the smallest pieces first.
[ 12, 8, 9, 3, 11, 5, 4]
[ 12, 8, 9] [ 3, 11, 5, 4]
[ 12] [ 8, 9] [ 3, 11, 5, 4]
[ 12] [ 8] [ 9] [ 3, 11, 5, 4]
Step 2: The splitting of the first sub-array is finished, and now it is time to merge. 8 and 9 are the first two elements to be merged. 8 is the lowest value, so that comes before 9 in the first merged sub-array.
[ 12] [ 8, 9] [ 3, 11, 5, 4]
Step 3: The next sub-arrays to be merged is [ 12] and [ 8, 9]. Values in both arrays are compared from the start. 8 is lower than 12, so 8 comes first, and 9 is also lower than 12.
[ 8, 9, 12] [ 3, 11, 5, 4]
Step 4: Now the second big sub-array is split recursively.
[ 8, 9, 12] [ 3, 11, 5, 4]
[ 8, 9, 12] [ 3, 11] [ 5, 4]
[ 8, 9, 12] [ 3] [ 11] [ 5, 4]
Step 5: 3 and 11 are merged back together in the same order as they are shown because 3 is lower than 11.
[ 8, 9, 12] [ 3, 11] [ 5, 4]
Step 6: Sub-array with values 5 and 4 is split, then merged so that 4 comes before 5.
[ 8, 9, 12] [ 3, 11] [ 5] [ 4]
[ 8, 9, 12] [ 3, 11] [ 4, 5]
Step 7: The two sub-arrays on the right are merged. Comparisons are done to create elements in the new merged array:
- 3 is lower than 4
- 4 is lower than 11
- 5 is lower than 11
- 11 is the last remaining value
[ 8, 9, 12] [ 3, 4, 5, 11]
Step 8: The two last remaining sub-arrays are merged. Let's look at how the comparisons are done in more detail to create the new merged and finished sorted array:
3 is lower than 8:
Before [ 8, 9, 12] [ 3, 4, 5, 11]
After: [ 3, 8, 9, 12] [ 4, 5, 11]
Step 9: 4 is lower than 8:
Before [ 3, 8, 9, 12] [ 4, 5, 11]
After: [ 3, 4, 8, 9, 12] [ 5, 11]
Step 10: 5 is lower than 8:
Before [ 3, 4, 8, 9, 12] [ 5, 11]
After: [ 3, 4, 5, 8, 9, 12] [ 11]
Step 11: 8 and 9 are lower than 11:
Before [ 3, 4, 5, 8, 9, 12] [ 11]
After: [ 3, 4, 5, 8, 9, 12] [ 11]
Step 12: 11 is lower than 12:
Before [ 3, 4, 5, 8, 9, 12] [ 11]
After: [ 3, 4, 5, 8, 9, 11, 12]
The sorting is finished!
Run the simulation below to see the steps above animated:
{{ x.dieNmbr }}
Manual Run Through: What Happened?
We see that the algorithm has two stages: first splitting, then merging.
Although it is possible to implement the Merge Sort algorithm without recursion, we will use recursion because that is the most common approach.
We cannot see it in the steps above, but to split an array in two, the length of the array is divided by two, and then rounded down to get a value we call "mid". This "mid" value is used as an index for where to split the array.
After the array is split, the sorting function calls itself with each half, so that the array can be split again recursively. The splitting stops when a sub-array only consists of one element.
At the end of the Merge Sort function the sub-arrays are merged so that the sub-arrays are always sorted as the array is built back up. To merge two sub-arrays so that the result is sorted, the values of each sub-array are compared, and the lowest value is put into the merged array. After that the next value in each of the two sub-arrays are compared, putting the lowest one into the merged array.
Merge Sort Implementation
To implement the Merge Sort algorithm we need:
- An array with values that needs to be sorted.
- A function that takes an array, splits it in two, and calls itself with each half of that array so that the arrays are split again and again recursively, until a sub-array only consist of one value.
- Another function that merges the sub-arrays back together in a sorted way.
The resulting code looks like this:
Example
def mergeSort(arr):
if len(arr) <= 1:
return arr
mid = len(arr) // 2
leftHalf = arr[:mid]
rightHalf = arr[mid:]
sortedLeft = mergeSort(leftHalf)
sortedRight = mergeSort(rightHalf)
return merge(sortedLeft, sortedRight)
def merge(left, right):
result = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result.extend(left[i:])
result.extend(right[j:])
return result
unsortedArr = [3, 7, 6, -10, 15, 23.5, 55, -13]
sortedArr = mergeSort(unsortedArr)
print("Sorted array:", sortedArr)On line 6, arr[:mid] takes all values from the array up until, but not including, the value on index "mid".
On line 7, arr[mid:] takes all values from the array, starting at the value on index "mid" and all the next values.
On lines 26-27, the first part of the merging is done. At this this point the values of the two sub-arrays are compared, and either the left sub-array or the right sub-array is empty, so the result array can just be filled with the remaining values from either the left or the right sub-array. These lines can be swapped, and the result will be the same.
Merge Sort without Recursion
Since Merge Sort is a divide and conquer algorithm, recursion is the most intuitive code to use for implementation. The recursive implementation of Merge Sort is also perhaps easier to understand, and uses less code lines in general.
But Merge Sort can also be implemented without the use of recursion, so that there is no function calling itself.
Take a look at the Merge Sort implementation below, that does not use recursion:
Example
def merge(left, right):
result = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result.extend(left[i:])
result.extend(right[j:])
return result
def mergeSort(arr):
step = 1 # Starting with sub-arrays of length 1
length = len(arr)
while step < length:
for i in range(0, length, 2 * step):
left = arr[i:i + step]
right = arr[i + step:i + 2 * step]
merged = merge(left, right)
# Place the merged array back into the original array
for j, val in enumerate(merged):
arr[i + j] = val
step *= 2 # Double the sub-array length for the next iteration
return arr
unsortedArr = [3, 7, 6, -10, 15, 23.5, 55, -13]
sortedArr = mergeSort(unsortedArr)
print("Sorted array:", sortedArr)
You might notice that the merge functions are exactly the same in the two Merge Sort implementations above, but in the implementation right above here the while loop inside the mergeSort function is used to replace the recursion. The while loop does the splitting and merging of the array in place, and that makes the code a bit harder to understand.
To put it simply, the while loop inside the mergeSort function uses short step lengths to sort tiny pieces (sub-arrays) of the initial array using the merge function. Then the step length is increased to merge and sort larger pieces of the array until the whole array is sorted.
Merge Sort Time Complexity
For a general explanation of what time complexity is, visit this page.
For a more thorough and detailed explanation of Merge Sort time complexity, visit this page.
The time complexity for Merge Sort is
\[ O( n \cdot \log n ) \]
And the time complexity is pretty much the same for different kinds of arrays. The algorithm needs to split the array and merge it back together whether it is already sorted or completely shuffled.
The image below shows the time complexity for Merge Sort.
Run the simulation below for different number of values in an array, and see how the number of operations Merge Sort needs on an array of \(n\) elements is \(O(n \log n)\):
{{ this.userX }}
Operations: {{ operations }}
If we hold the number of values \(n\) fixed, the number of operations needed for the "Random", "Descending" and "Ascending" is almost the same.
Merge Sort performs almost the same every time because the array is split, and merged using comparison, both if the array is already sorted or not.

