DSA Linear Search Time Complexity
See this page for a general explanation of what time complexity is.
Linear Search Time Complexity
For a general explanation of what time complexity is, visit this page.
For a more thorough and detailed explanation of Insertion Sort time complexity, visit this page.
Linear Search compares each value with the value it is looking for. If the value is found, the index is returned, and if it is not found -1 is returned.
To find the time complexity for Linear Search, let's see if we can fins out how many compare operations are needed to find a value in an array with \(n\) values.
Best Case Scenario is if the value we are looking for is the first value in the array. In such a case only one compare is needed and the time complexity is \(O(1)\).
Worst Case Scenario is if the whole array is looked through without finding the target value. In such a case all values in the array are compared with the target value, and the time complexity is \(O(n)\).
Average Case Scenario is not so easy to pinpoint. What is the possibility to finding the target value? That depends on the values in the array right? But if we assume that exactly one of the values in the array is equal to the target value, and that the position of that value can be anywhere, the average time needed for Linear Search is half of the time time needed in the worst case scenario.
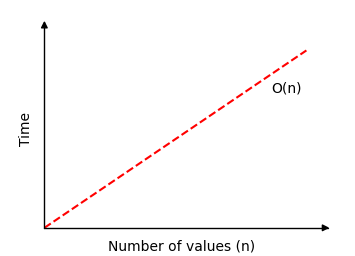
Time complexity for Linear Search is \(O(n)\).
If we draw how much time Linear Search needs to find a value in an array of \(n\) values, we get this graph:
Linear Search Simulation
Run the simulation for different number of values in an array, and see how many compares are needed for Linear Search to find a value in an array of \(n\) values:
{{ this.userX }}
Operations: {{ operations }}
Not found!
As you can see when running simulations of Linear Search, the search requires few compares if the value is found fast, but if the value we are looking for is not found, the maximum of compares are done.

