DSA Quicksort

Quicksort

As the name suggests, Quicksort is one of the fastest sorting algorithms.

The Quicksort algorithm takes an array of values, chooses one of the values as the 'pivot' element, and moves the other values so that lower values are on the left of the pivot element, and higher values are on the right of it.

In this tutorial the last element of the array is chosen to be the pivot element, but we could also have chosen the first element of the array, or any element in the array really.

Then, the Quicksort algorithm does the same operation recursively on the sub-arrays to the left and right side of the pivot element. This continues until the array is sorted.

The algorithm can be described like this:

Continue reading to fully understand the Quicksort algorithm and how to implement it yourself.

Manual Run Through

Before we implement the Quicksort algorithm in a programming language, let's manually run through a short array, just to get the idea.

Step 1: We start with an unsorted array.

Step 2: We choose the last value 3 as the pivot element.

Step 3: The rest of the values in the array are all lower than 3, an must be on the right side of 3. Swap 3 with 11.

Step 4: Value 3 is now in the correct position. We need to sort the values to the right of 3. We choose the last value 11 as the new pivot element.

Step 5: The value 7 must be to the left of pivot value 11, and 12 must be to the right of it. Move 7 and 12.

Step 6: Swap 11 with 12 so that lower values 9 anf 7 are on the left side of 11, and 12 is on the right side.

Step 7: 11 and 12 are in the correct positions. We choose 7 as the pivot element in sub-array [ 9, 7], to the left of 11.

Step 8: We must swap 9 with 7.

And now, the array is sorted.

Run the simulation below to see the steps above animated:

Manual Run Through: What Happened?

Before we implement the algorithm in a programming language we need to go through what happened above in more detail.

We have already seen that last value of the array is chosen as the pivot element, and the rest of the values are arranged so that the values lower than the pivot value are to the left, and the higher values are to the right.

After that, the pivot element is swapped with the first of the higher values. This splits the original array in two, with the pivot element in between the lower and the higher values.

Now we need to do the same as above with the sub-arrays on the left and right side of the old pivot element. And if a sub-array has length 0 or 1, we consider it finished sorted.

To sum up, the Quicksort algorithm makes the sub-arrays become shorter and shorter until array is sorted.

Quicksort Implementation

To write a 'quickSort' method that splits the array into shorter and shorter sub-arrays we use recursion. This means that the 'quickSort' method must call itself with the new sub-arrays to the left and right of the pivot element. Read more about recursion here.

To implement the Quicksort algorithm in a programming language, we need:

1. An array with values to sort.
2. A quickSort method that calls itself (recursion) if the sub-array has a size larger than 1.
3. A partition method that receives a sub-array, moves values around, swaps the pivot element into the sub-array and returns the index where the next split in sub-arrays happens.

The resulting code looks like this:

def partition(array, low, high):
    pivot = array[high]
    i = low - 1

    for j in range(low, high):
        if array[j] <= pivot:
            i += 1
            array[i], array[j] = array[j], array[i]

    array[i+1], array[high] = array[high], array[i+1]
    return i+1

def quicksort(array, low=0, high=None):
    if high is None:
        high = len(array) - 1

    if low < high:
        pivot_index = partition(array, low, high)
        quicksort(array, low, pivot_index-1)
        quicksort(array, pivot_index+1, high)

my_array = [64, 34, 25, 12, 22, 11, 90, 5]
quicksort(my_array)
print("Sorted array:", my_array)

Quicksort Time Complexity

For a general explanation of what time complexity is, visit this page.

For a more thorough and detailed explanation of Quicksort time complexity, visit this page.

The worst case scenario for Quicksort is \(O(n^2) \). This is when the pivot element is either the highest or lowest value in every sub-array, which leads to a lot of recursive calls. With our implementation above, this happens when the array is already sorted.

But on average, the time complexity for Quicksort is actually just \(O(n \log n) \), which is a lot better than for the previous sorting algorithms we have looked at. That is why Quicksort is so popular.

Below you can see the significant improvement in time complexity for Quicksort in an average scenario \(O(n \log n) \), compared to the previous sorting algorithms Bubble, Selection and Insertion Sort with time complexity \(O(n^2) \):

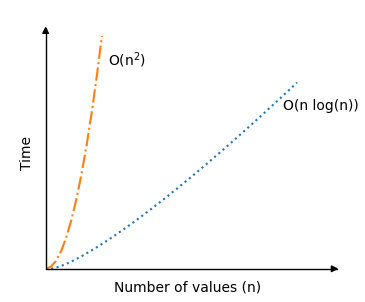
The recursion part of the Quicksort algorithm is actually a reason why the average sorting scenario is so fast, because for good picks of the pivot element, the array will be split in half somewhat evenly each time the algorithm calls itself. So the number of recursive calls do not double, even if the number of values \(n \) double.

Run Quicksort on different kinds of arrays with different number of values in the simulation below:

def partition(array, low, high):
    pivot = array[high]
    i = low - 1

    for j in range(low, high):
        if array[j] <= pivot:
            i += 1
            array[i], array[j] = array[j], array[i]

    array[i+1], array[high] = array[high], array[i+1]
    return i+1

def quicksort(array, low=0, high=None):
    if high is None:
        high = len(array) - 1

    if low < high:
        pivot_index = partition(array, low, high)
        (array, low, pivot_index-1)
        (array, pivot_index+1, high)

my_array = [64, 34, 25, 12, 22, 11, 90, 5]
quicksort(my_array)
print("Sorted array:", my_array)