DSA Selection Sort Time Complexity
See this page for a general explanation of what time complexity is.
Binary Search Time Complexity
Binary Search finds the target value in an already sorted array by checking the center value. If the center value is not the target value, Linear Search selects the left or right sub-array and continues the search until the target value is found.
To find the time complexity for Binary Search, let's see how many compare operations are needed to find the target value in an array with \(n\) values.
The best case scenario is if the first middle value is the same as the target value. If this happens the target value is found straight away, with only one compare, so the time complexity is \(O(1)\) in this case.
The worst case scenario is if the search area must be cut in half over and over until the search area is just one value. When this happens, it does not affect the time complexity if the target value is found or not.
Let's consider array lengths that are powers of 2, like 2, 4, 8, 16, 32 64 and so on.
How many times must 2 be cut in half until we are looking at just one value? It is just one time, right?
How about 8? We must cut an array of 8 values in half 3 times to arrive at just one value.
An array of 32 values must be cut in half 5 times.
We can see that \(2=2^1\), \(8=2^3\) and \(32=2^5\). So the number of times we must cut an array to arrive at just one element can be found in the power with base 2. Another way to look at it is to ask "how many times must I multiply 2 with itself to arrive at this number?". Mathematically we can use the base-2 logarithm, so that we can find out that an array of length \(n\) can be split in half \( \log_{2}(n)\) times.
This means that time complexity for Binary Search is
\[ \underline{\underline{O( \log_{2} n )}} \]
The average case scenario is not so easy to pinpoint, but since we understand time complexity of an algorithm as the upper bound of the worst case scenario, using Big O notation, the average case scenario is not that interesting.
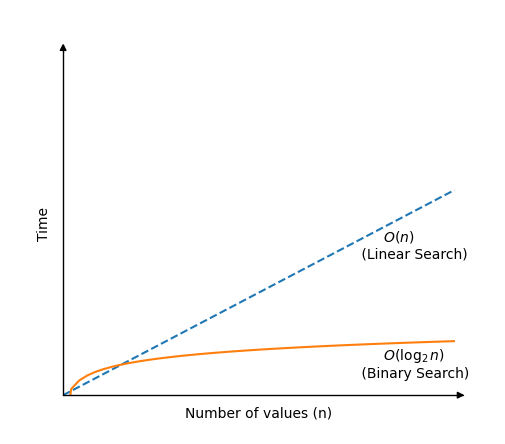
Note: Time complexity for Binary Search \(O( \log_{2}n)\) is a lot faster than Linear Search \(O(n)\), but it is important to remember that Binary Search requires a sorted array, and Linear Search does not.
If we draw how much time Binary Search needs to find a value in an array of \(n\) values, compared to Linear Search, we get this graph:
Binary Search Simulation
Run the simulation for different number of values \(n\) in an array, and see how many compares are needed for Binary Search to find the target value:
{{ this.userX }}
Operations: {{ operations }}
Not found!
As you can see when running simulations of Binary Search, the search requires very few compares, even if the the array is big and the value we are looking for is not found.

