DSA Radix Sort
Radix Sort
The Radix Sort algorithm sorts an array by individual digits, starting with the least significant digit (the rightmost one).
Click the button to do Radix Sort, one step (digit) at a time.
{{ msgDone }}The radix (or base) is the number of unique digits in a number system. In the decimal system we normally use, there are 10 different digits from 0 till 9.
Radix Sort uses the radix so that decimal values are put into 10 different buckets (or containers) corresponding to the digit that is in focus, then put back into the array before moving on to the next digit.
Radix Sort is a non comparative algorithm that only works with non negative integers.
The Radix Sort algorithm can be described like this:
How it works:
- Start with the least significant digit (rightmost digit).
- Sort the values based on the digit in focus by first putting the values in the correct bucket based on the digit in focus, and then put them back into array in the correct order.
- Move to the next digit, and sort again, like in the step above, until there are no digits left.
Stable Sorting
Radix Sort must sort the elements in a stable way for the result to be sorted correctly.
A stable sorting algorithm is an algorithm that keeps the order of elements with the same value before and after the sorting. Let's say we have two elements "K" and "L", where "K" comes before "L", and they both have value "3". A sorting algorithm is considered stable if element "K" still comes before "L" after the array is sorted.
It makes little sense to talk about stable sorting algorithms for the previous algorithms we have looked at individually, because the result would be same if they are stable or not. But it is important for Radix Sort that the the sorting is done in a stable way because the elements are sorted by just one digit at a time.
So after sorting the elements on the least significant digit and moving to the next digit, it is important to not destroy the sorting work that has already been done on the previous digit position, and that is why we need to take care that Radix Sort does the sorting on each digit position in a stable way.
In the simulation below it is revealed how the underlying sorting into buckets is done. And to get a better understanding of how stable sorting works, you can also choose to sort in an unstable way, that will lead to an incorrect result. The sorting is made unstable by simply putting elements into buckets from the end of the array instead of from the start of the array.
Speed:
Stable sort?
{{ msgDone }}Manual Run Through
Let's try to do the sorting manually, just to get an even better understanding of how Radix Sort works before actually implementing it in a programming language.
Step 1: We start with an unsorted array, and an empty array to fit values with corresponding radices 0 till 9.
myArray = [ 33, 45, 40, 25, 17, 24]
radixArray = [ [], [], [], [], [], [], [], [], [], [] ]
Step 2: We start sorting by focusing on the least significant digit.
myArray = [ 33, 45, 40, 25, 17, 24]
radixArray = [ [], [], [], [], [], [], [], [], [], [] ]
Step 3: Now we move the elements into the correct positions in the radix array according to the digit in focus. Elements are taken from the start of myArray and pushed into the correct position in the radixArray.
myArray = [ ]
radixArray = [ [40], [], [], [33], [24], [45, 25], [], [17], [], [] ]
Step 4: We move the elements back into the initial array, and the sorting is now done for the least significant digit. Elements are taken from the end radixArray, and put into the start of myArray.
myArray = [ 40, 33, 24, 45, 25, 17 ]
radixArray = [ [], [], [], [], [], [], [], [], [], [] ]
Step 5: We move focus to the next digit. Notice that values 45 and 25 are still in the same order relative to each other as they were to start with, because we sort in a stable way.
myArray = [ 40, 33, 24, 45, 25, 17 ]
radixArray = [ [], [], [], [], [], [], [], [], [], [] ]
Step 6: We move elements into the radix array according to the focused digit.
myArray = [ ]
radixArray = [ [], [17], [24, 25], [33], [40, 45], [], [], [], [], [] ]
Step 7: We move elements back into the start of myArray, from the back of radixArray.
myArray = [ 17, 24, 25, 33, 40, 45 ]
radixArray = [ [], [], [], [], [], [], [], [], [], [] ]
The sorting is finished!
Run the simulation below to see the steps above animated:
radixArray = [ [
Manual Run Through: What Happened?
We see that values are moved from the array and placed in the radix array according to the current radix in focus. And then the values are moved back into the array we want to sort.
This moving of values from the array we want to sort and back again must be done as many times as the maximum number of digits in a value. So for example if 437 is the highest number in the array that needs to be sorted, we know we must sort three times, once for each digit.
We also see that the radix array needs to be two-dimensional so that more than one value on a specific radix, or index.
And, as mentioned earlier, we must move values between the two arrays in a way that keeps the order of values with the same radix in focus, so the the sorting is stable.
Radix Sort Implementation
To implement the Radix Sort algorithm we need:
- An array with non negative integers that needs to be sorted.
- A two dimensional array with index 0 to 9 to hold values with the current radix in focus.
- A loop that takes values from the unsorted array and places them in the correct position in the two dimensional radix array.
- A loop that puts values back into the initial array from the radix array.
- An outer loop that runs as many times as there are digits in the highest value.
The resulting code looks like this:
Example
myArray = [170, 45, 75, 90, 802, 24, 2, 66]
print("Original array:", myArray)
radixArray = [[], [], [], [], [], [], [], [], [], []]
maxVal = max(myArray)
exp = 1
while maxVal // exp > 0:
while len(myArray) > 0:
val = myArray.pop()
radixIndex = (val // exp) % 10
radixArray[radixIndex].append(val)
for bucket in radixArray:
while len(bucket) > 0:
val = bucket.pop()
myArray.append(val)
exp *= 10
print("Sorted array:", myArray)On line 7, we use floor division ("//") to divide the maximum value 802 by 1 the first time the while loop runs, the next time it is divided by 10, and the last time it is divided by 100. When using floor division "//", any number beyond the decimal point are disregarded, and an integer is returned.
On line 11, it is decided where to put a value in the radixArray based on its radix, or digit in focus. For example, the second time the outer while loop runs exp will be 10. Value 170 divided by 10 will be 17. The "%10" operation divides by 10 and returns what is left. In this case 17 is divided by 10 one time, and 7 is left. So value 170 is placed in index 7 in the radixArray.
Radix Sort Using Other Sorting Algorithms
Radix Sort can actually be implemented together with any other sorting algorithm as long as it is stable. This means that when it comes down to sorting on a specific digit, any stable sorting algorithm will work, such as counting sort or bubble sort.
This is an implementation of Radix Sort that uses Bubble Sort to sort on the individual digits:
Example
def bubbleSort(arr):
n = len(arr)
for i in range(n):
for j in range(0, n - i - 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
def radixSortWithBubbleSort(arr):
max_val = max(arr)
exp = 1
while max_val // exp > 0:
radixArray = [[],[],[],[],[],[],[],[],[],[]]
for num in arr:
radixIndex = (num // exp) % 10
radixArray[radixIndex].append(num)
for bucket in radixArray:
bubbleSort(bucket)
i = 0
for bucket in radixArray:
for num in bucket:
arr[i] = num
i += 1
exp *= 10
myArray = [170, 45, 75, 90, 802, 24, 2, 66]
print("Original array:", myArray)
radixSortWithBubbleSort(myArray)
print("Sorted array:", myArray)
Radix Sort Time Complexity
For a general explanation of what time complexity is, visit this page.
For a more thorough and detailed explanation of Radix Sort time complexity, visit this page.
The time complexity for Radix Sort is:
\[ \underline{\underline{O(n \cdot k)}} \]
This means that Radix Sort depends both on the values that need to be sorted \(n\), and the number of digits in the highest value \(k\).
A best case scenario for Radix Sort is if there are lots of values to sort, but the values have few digits. For example if there are more than a million values to sort, and the highest value is 999, with just three digits. In such a case the time complexity \(O(n \cdot k)\) can be simplified to just \(O(n)\).
A worst case scenario for Radix Sort would be if there are as many digits in the highest value as there are values to sort. This is perhaps not a common scenario, but the time complexity would be \(O(n^2)\)in this case.
The most average or common case is perhaps if the number of digits \(k\) is something like \(k(n)= \log n\). If so, Radix Sort gets time complexity \(O(n \cdot \log n )\). An example of such a case would be if there are 1000000 values to sort, and the values have 6 digits.
See different possible time complexities for Radix Sort in the image below.
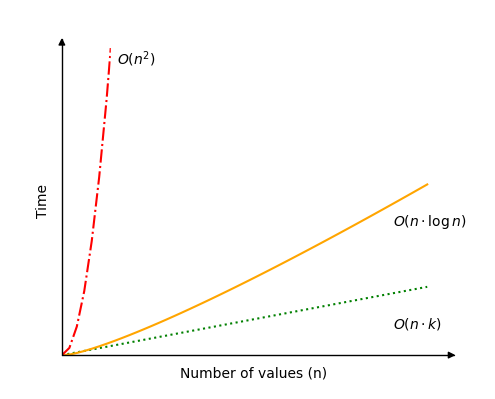
Run different simulations of Radix Sort to see how the number of operations falls between the worst case scenario \(O(n^2)\) (red line) and best case scenario \(O(n)\) (green line).
{{ this.userX }}
{{ this.userK }}
Operations: {{ operations }}
The bars representing the different values are scaled to fit the window, so that it looks ok. This means that values with 7 digits look like they are just 5 times bigger than values with 2 digits, but in reality, values with 7 digits are actually 5000 times bigger than values with 2 digits!
If we hold \(n\) and \(k\) fixed, the "Random", "Descending" and "Ascending" alternatives in the simulation above results in the same number of operations. This is because the same thing happens in all three cases.

