DSA Insertion Sort
Insertion Sort
The Insertion Sort algorithm uses one part of the array to hold the sorted values, and the other part of the array to hold values that are not sorted yet.
Speed:
{{ msgDone }}The algorithm takes one value at a time from the unsorted part of the array and puts it into the right place in the sorted part of the array, until the array is sorted.
How it works:
- Take the first value from the unsorted part of the array.
- Move the value into the correct place in the sorted part of the array.
- Go through the unsorted part of the array again as many times as there are values.
Continue reading to fully understand the Insertion Sort algorithm and how to implement it yourself.
Manual Run Through
Before we implement the Insertion Sort algorithm in a programming language, let's manually run through a short array, just to get the idea.
Step 1: We start with an unsorted array.
[ 7, 12, 9, 11, 3]
Step 2: We can consider the first value as the initial sorted part of the array. If it is just one value, it must be sorted, right?
[ 7, 12, 9, 11, 3]
Step 3: The next value 12 should now be moved into the correct position in the sorted part of the array. But 12 is higher than 7, so it is already in the correct position.
[ 7, 12, 9, 11, 3]
Step 4: Consider the next value 9.
[ 7, 12, 9, 11, 3]
Step 5: The value 9 must now be moved into the correct position inside the sorted part of the array, so we move 9 in between 7 and 12.
[ 7, 9, 12, 11, 3]
Step 6: The next value is 11.
[ 7, 9, 12, > 11, 3]
Step 7: We move it in between 9 and 12 in the sorted part of the array.
[ 7, 9, 11, 12, 3]
Step 8: The last value to insert into the correct position is 3.
[ 7, 9, 11, 12, 3]
Step 9: We insert 3 in front of all other values because it is the lowest value.
[ 3,7, 9, 11, 12]
Finally, the array is sorted.
Run the simulation below to see the steps above animated:
Manual Run Through: What Happened?
We must understand what happened above to fully understand the algorithm, so that we can implement the algorithm in a programming language.
The first value is considered to be the initial sorted part of the array.
Every value after the first value must be compared to the values in the sorted part of the algorithm so that it can be inserted into the correct position.
The Insertion Sort Algorithm must run through the array 4 times, to sort the array of 5 values because we do not have to sort the first value.
And each time the algorithm runs through the array, the remaining unsorted part of the array becomes shorter.
We will now use what we have learned to implement the Insertion Sort algorithm in a programming language.
Insertion Sort Implementation
To implement the Insertion Sort algorithm in a programming language, we need:
- An array with values to sort.
- An outer loop that picks a value to be sorted. For an array with \(n\) values, this outer loop skips the first value, and must run \(n-1\) times.
- An inner loop that goes through the sorted part of the array, to find where to insert the value. If the value to be sorted is at index \(i\), the sorted part of the array starts at index \(0\) and ends at index \(i-1\).
The resulting code looks like this:
Example
my_array = [64, 34, 25, 12, 22, 11, 90, 5]
n = len(my_array)
for i in range(1,n):
insert_index = i
current_value = my_array.pop(i)
for j in range(i-1, -1, -1):
if my_array[j] > current_value:
insert_index = j
my_array.insert(insert_index, current_value)
print("Sorted array:", my_array)
Insertion Sort Improvement
Insertion Sort can be improved a little bit more.
The way the code above first removes a value and then inserts it somewhere else is intuitive. It is how you would do Insertion Sort physically with a hand of cards for example. If low value cards are sorted to the left, you pick up a new unsorted card, and insert it in the correct place between the other already sorted cards.
The problem with this way of programming it is that when removing a value from the array, all elements above must be shifted one index place down:
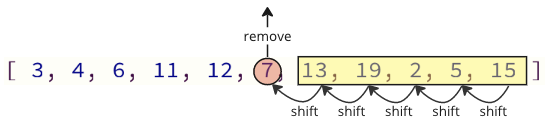
And when inserting the removed value into the array again, there are also many shift operations that must be done: all following elements must shift one position up to make place for the inserted value:
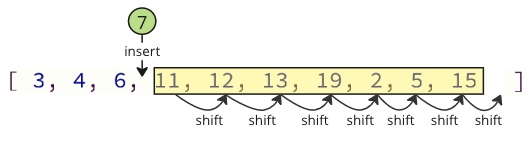
These shifting operations can take a lot of time, especially for an array with many elements.
Hidden memory shifts: You will not see these shifting operations happening in the code if you are using a high-level programming language such as Python or JavaScript, but the shifting operations are still happening in the background. Such shifting operations require extra time for the computer to do, which can be a problem.
You can read more about how arrays are stored in memory here.
C and Java code examples above and below are the same: The issue of memory shifts happening behind the scenes is only relevant for high-level programming languages like Python or JavaScript, where arrays are dynamic, which means you can easily remove and insert elements. In lower-level programming languages like C and Java, where arrays have a fixed length, elements cannot be removed or inserted. As a result, there are no such memory shifts happening, and therefore the example codes above and below for C and Java remain the same.
Improved Solution
We can avoid most of these shift operations by only shifting the values necessary:
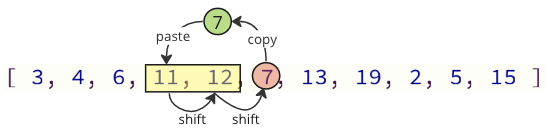
In the image above, first value 7 is copied, then values 11 and 12 are shifted one place up in the array, and at last value 7 is put where value 11 was before.
The number of shifting operations is reduced from 12 to 2 in this case.
This improvement is implemented in the example below:
Example
my_array = [64, 34, 25, 12, 22, 11, 90, 5]
n = len(my_array)
for i in range(1,n):
insert_index = i
current_value = my_array[i]
for j in range(i-1, -1, -1):
if my_array[j] > current_value:
my_array[j+1] = my_array[j]
insert_index = j
else:
break
my_array[insert_index] = current_value
print("Sorted array:", my_array)What is also done in the code above is to break out of the inner loop. That is because there is no need to continue comparing values when we have already found the correct place for the current value.
Insertion Sort Time Complexity
For a general explanation of what time complexity is, visit this page.
For a more thorough and detailed explanation of Insertion Sort time complexity, visit this page.
Insertion Sort sorts an array of \(n\) values.
On average, each value must be compared to about \(\frac{n}{2}\) other values to find the correct place to insert it.
Insertion Sort must run the loop to insert a value in its correct place approximately \(n\) times.
We get time complexity for Insertion Sort:
\[ O( \frac{n}{2} \cdot n) = \underline{\underline{O(n^2)}} \]
The time complexity for Insertion Sort can be displayed like this:
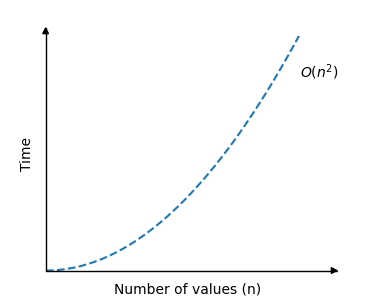
Use the simulation below to see how the theoretical time complexity \(O(n^2)\) (red line) compares with the number of operations of actual Insertion Sorts.
{{ this.userX }}
Operations: {{ operations }}
For Insertion Sort, there is a big difference between best, average and worst case scenarios. You can see that by running the different simulations above.
Next up is Quicksort. Finally we will see a faster sorting algorithm!

