DSA Arrays
Arrays
An array is a data structure used to store multiple elements.
Arrays are used by many algorithms.
For example, an algorithm can be used to look through an array to find the lowest value, like the animation below shows:
Speed:
{{ msgDone }}Lowest value: {{ minVal }}
In Python, an array can be created like this:
my_array = [7, 12, 9, 4, 11]Note: The Python code above actually generates a Python 'list' data type, but for the scope of this tutorial the 'list' data type can be used in the same way as an array. Learn more about Python lists here.
Arrays are indexed, meaning that each element in the array has an index, a number that says where in the array the element is located. The programming languages in this tutorial (Python, Java, and C) use zero-based indexing for arrays, meaning that the first element in an array can be accessed at index 0.
In Python, this code use index 0 to write the first array element (value 7) to the console:
Algorithm: Find The Lowest Value in an Array
Let's create our first algorithm using the array data structure.
Below is the algorithm to find the lowest number in an array.
How it works:
- Go through the values in the array one by one.
- Check if the current value is the lowest so far, and if it is, store it.
- After looking at all the values, the stored value will be the lowest of all values in the array.
Try the simulation below to see how the algorithm for finding the lowest value works (the animation is the same as the one on the top of this page):
Speed:
{{ msgDone }}Lowest value: {{ minVal }}
This next simulation also finds the lowest value in an array, just like the simulation above, but here we can see how the numbers inside the array are checked to find the lowest value:
Implementation
Before implementing the algorithm using an actual programming language, it is usually smart to first write the algorithm as a step-by-step procedure.
If you can write down the algorithm in something between human language and programming language, the algorithm will be easier to implement later because we avoid drowning in all the details of the programming language syntax.
- Create a variable 'minVal' and set it equal to the first value of the array.
- Go through every element in the array.
- If the current element has a lower value than 'minVal', update 'minVal' to this value.
- After looking at all the elements in the array, the 'minVal' variable now contains the lowest value.
You can also write the algorithm in a way that looks more like a programming language if you want to, like this:
Variable 'minVal' = array[0]
For each element in the array
If current element < minVal
minVal = current element
Note: The two step-by-step descriptions of the algorithm we have written above can be called 'pseudocode'. Pseudocode is a description of what a program does, using language that is something between human language and a programming language.
After we have written down the algorithm, it is much easier to implement the algorithm in a specific programming language:
Example
Python:
my_array = [7, 12, 9, 4, 11]
minVal = my_array[0] # Step 1
for i in my_array: # Step 2
if i < minVal: # Step 3
minVal = i
print('Lowest value: ',minVal) # Step 4Algorithm Time Complexity
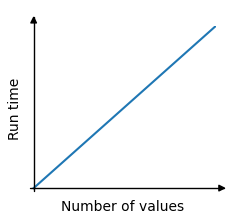
When exploring algorithms, we often look at how much time an algorithm takes to run relative to the size of the data set.
In the example above, the time the algorithm needs to run is proportional, or linear, to the size of the data set. This is because the algorithm must visit every array element one time to find the lowest value. The loop must run 5 times since there are 5 values in the array. And if the array had 1000 values, the loop would have to run 1000 times.
Try the simulation below to see this relationship between the number of compare operations needed to find the lowest value, and the size of the array.
See this page for a more thorough explanation of what time complexity is.
Each algorithm in this tutorial will be presented together with its time complexity.
{{ this.userX }}
Operations: {{ operations }}

