DSA Radix Sort Time Complexity
See this page for a general explanation of what time complexity is.
Radix Sort Time Complexity
The Radix Sort algorithm sorts non negative integers, one digit at a time.
There are \(n\) values that need to be sorted, and \(k\) is the number of digits in the highest value.
When Radix Sort runs, every value is moved to the radix array, and then every value is moved back into the initial array. So \(n\) values are moved into the radix array, and \(n\) values are moved back. This gives us \(n + n=2 \cdot n\) operations.
And the moving of values as described above needs to be done for every digit. This gives us a total of \(2 \cdot n \cdot k\) operations.
This gives us time complexity for Radix Sort:
\[ O(2 \cdot n \cdot k) = \underline{\underline{O(n \cdot k)}} \]
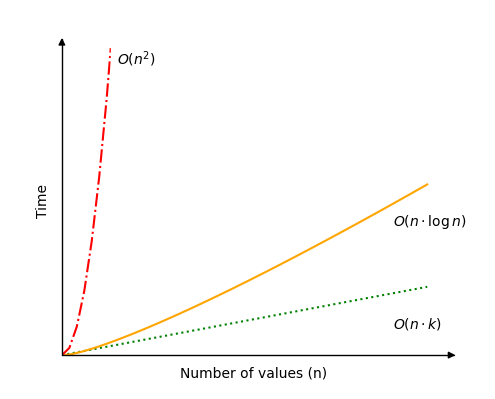
Radix Sort is perhaps the fastest sorting algorithms there is, as long as the number of digits \(k\) is kept relatively small compared to the number of values \(n\).
We can imagine a scenario where the number of digits \(k\) is the same as the number of values \(n\), in such a case we get time complexity \(O(n \cdot k)=O(n^2)\) which is quite slow, and has the same time complexity as for example Bubble Sort.
We can also image a scenario where the number of digits \(k\) grow as the number of values \(n\) grow, so that \(k(n)= \log n\). In such a scenario we get time complexity \(O(n \cdot k)=O(n \cdot \log n )\), which is the same as for example Quicksort.
See the time complexity for Radix Sort in the image below.
Radix Sort Simulation
Run different simulations of Radix Sort to see how the number of operations falls between the worst case scenario \(O(n^2)\) (red line) and best case scenario \(O(n)\) (green line).
{{ this.userX }}
{{ this.userK }}
Operations: {{ operations }}
The bars representing the different values are scaled to fit the window, so that it looks ok. This means that values with 7 digits look like they are just 5 times bigger than values with 2 digits, but in reality, values with 7 digits are actually 5000 times bigger than values with 2 digits!
If we hold \(n\) and \(k\) fixed, the "Random", "Descending" and "Ascending" alternatives in the simulation above results in the same number of operations. This is because the same thing happens in all three cases.

